jinyux’s diary

IT業界初心者です。勉強したことをまとめています。

主加法標準形・主乗法標準形

ハードウェア ブール代数 ディジタル回路設計とコンピュータアーキテクチャ

先日の投稿（ANDアレイ - jinyux’s diary）で説明したことについて少し勉強が進んだのでまたまとめてみる。内容的には単なる言い換えになってしまっているが、自分的に言葉の整理をしたいと思ったのである。

論理式に関する用語の説明

・最小項
論理関数への入力すべてを含む論理積のこと。例えば3変数A, B, Cの関数に対してA\bar{B}\bar{C}は最小項となるがA\bar{C}は最小項ではない。

・最大項
入力すべてを含む論理和のこと。A+\bar{B}+\bar{C}は3変数A, B, Cの関数の最大項である。

・主加法標準形
ある論理関数を最小項の論理和で表したものを主加法標準形という。これはまさに前述したすでに投稿した記事で説明したことの言い換えである。
例えば以下のような真理値表を考える時、2入力なので2^2行あるわけだが、この各行には入力のとり得るパターンが記入される。

A B E
0 0 1
1 0 0
0 1 0
1 1 0

この各行にTrueとなる最小項を記入すると以下のようになる。

A B E Trueとなる最小項
0 0 1 \bar{A}\bar{B}
1 0 0 A\bar{B}
0 1 0 \bar{A}B
1 1 0 AB

この論理関数の主加法標準形は出力がTrueとなる行の最小項を論理和でつなげたものだから
E=\bar{A}\bar{B}
となる。

・主乗法標準形
ある論理関数を最大項の論理積で表したものを主乗法標準形という。真理値表でいえば各行の入力に対してFalseとなる最大項を考えることである。

A B E Falseとなる最大項
0 0 1 A+B
1 0 0 \bar{A}+B
0 1 0 A+\bar{B}
1 1 0 \bar{A}+\bar{B}

主乗法標準形は出力がFalseになる行の最大項の論理積をとるので
E=(\bar{A}+B)(A+\bar{B})(\bar{A}+\bar{B})
となる。当然だがこれを展開すると主加法標準形と同じ形になる。
出力がTrueとなっている行が少なければ主加法標準形のほうが式が簡単であり、Falseとなる行が少なければ主乗法標準形のほうが簡単になる。

ALUの基本 その1

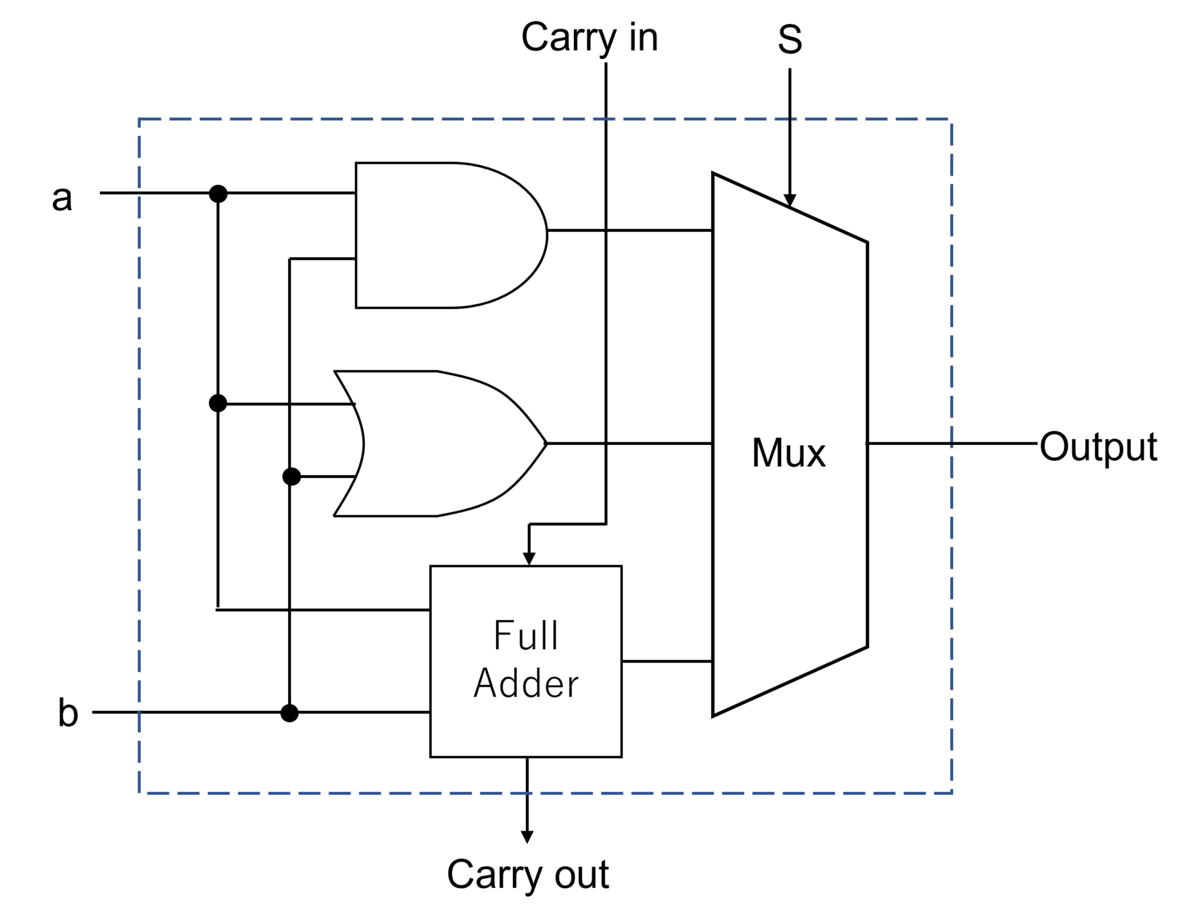
ハードウェア Introduction to Computing Systems

ALUとはArithmetic Logic Unit(算術論理演算装置)の頭文字で論理積、論理和、加算、減算を行う装置である。まず1bitの論理積・論理和と加算のみを行うALUを考えてみる。それは以下の図のようになる。入力をa, bとする。

構造としては単純でAND, ORゲートと全加算器の出力をMuxで選択して出力しているだけである。入力はa, bのほかにCarry in（下位桁からの繰り上がり）とMuxの選択信号Sが必要になる。出力はoutputとCarry out（上位桁への繰り上がり）となる。

このALUを組み合わせて32bitの演算を行うALUを作る。それは以下のようになる。

32bitの入力A, Bのそれぞれの桁をA_i, B_i (i = 0, 1, 2, \cdots 31)とし、それぞれのALUのCarry outを次の桁のCarry inに入力することで実現する。

さて、先程の1bit ALUに減算機能を追加する。a-bとはa+(-1)\cdot bという意味である。つまり引く方の正負を反転すれば良い。2進数において、正負を反転することには2の補数表現が利用できる。つまり、各桁のbitを反転させて1を加えればよい。まず、入力bを反転させるには最初の入力と反転させた信号を選択するMuxを追加する。

bitを反転させたあとは1を加えなければならない。これは1bit ALUであるが、実際は先程みたように複数個組み合わせて使う。そのとき、最下位bitに入力されるCarry inは本質的には意味がないものなので通常は0が入力される。しかし、補数表現をとるときに（Invert Bでbit反転を選択するとき）、1を入力するようにするとa+b+1となり、1加えることができる。これによって負の補数表現を実現することができ、減算が可能になる。

参考：コンピュータの構成と設計 第6版 下

加算器

ハードウェア Introduction to Computing Systems
半加算器

これから2進数の足し算を行う論理回路を考えてみる。まずは一桁の2進数の足し算を考える。2つの入力をA, Bとし、その和がS, 繰り上がりをCとする。すると真理値表は以下のようになる。

A B S C
0 0 0 0
1 0 1 0
0 1 1 0
1 1 0 1

真理値表のSに着目するとこれはA, BのXOR演算だとわかる。またCについてはAND演算である。よってこの回路は以下のようになる。

このような回路を半加算器と呼ぶ。半加算器は下位の桁からの繰り上がりを考慮できないので、複数桁の足し算を行うにはもっと改良が必要である。

全加算器

複数桁の足し算に対応した回路を考える。複数桁をもつ2つの2進数をA, Bとし、それぞれの右からi桁目（i=0, 1, 2, \cdots ）の数をA_i, B_iとする。そして下位桁からの繰り上がりをC_iする。そうするとA_i, B_i, C_iが入力となる。そして該当桁の和をS_i, 上位桁への繰り上がりをC_{i+1}とすると、S_i, C_{i+1}が出力となる。この場合の真理値表は以下のようになる。

A_i B_i C_i C_{i+1} S_i
0 0 0 0 0
1 0 0 0 1
0 1 0 0 1
1 1 0 1 0
0 0 1 0 1
1 0 1 1 0
0 1 1 1 0
1 1 1 1 1

このような回路を全加算器と呼ぶ。全加算器は半加算器の組み合わせで得られることが知られている。具体的には以下のようになる。

図中の半加算器と書かれた四角形は前述の半加算器をひとまとめにして表したものである。

複数桁の足し算を行う回路

前述の全加算器は一桁の足し算を行うので複数桁の足し算のためにはやはり全加算器を組み合わせて使う。以下の回路は4桁の足し算を行う回路である。全加算器の繰り上がり出力C_{i+1}が次の桁のC_iに入力する。この組み合わせで複数桁の計算を実現できる。このような1bit加算器を直接につなぎ合わせて作成した加算器を順次桁上げ加算器と呼ぶ。


ANDアレイをつかった全加算器回路

余談であるがANDアレイを使った全加算器回路を考えてみる。前回で示したとおり、ANDアレイをつかうと機械的に回路を実装できる。今回は出力がS_i, C_{i+1}の2つであり、それぞれの出力が1になるときの入力パターンを真理値表から対応付けていけば以下の回路が出てくる。

ANDアレイ

ハードウェア Introduction to Computing Systems

デコーダー回路で以下のような回路を見た。

この回路の真理値表は以下のようになる

A B C a b c d e f g h
0 0 0 1 0 0 0 0 0 0 0
0 0 1 0 1 0 0 0 0 0 0
0 1 0 0 0 1 0 0 0 0 0
0 1 1 0 0 0 1 0 0 0 0
1 0 0 0 0 0 0 1 0 0 0
1 0 1 0 0 0 0 0 1 0 0
1 1 0 0 0 0 0 0 0 1 0
1 1 1 0 0 0 0 0 0 0 1

A, B, Cの各入力パターンに対してa ～ hのどれかひとつが1になるパターンが1対1で対応している。これを利用すると自由にロジックを実装することができる。つまり、出力が1になってほしい入力パターン（つまりそれに対応したa ～ hの出力）をORゲートの入力に接続し、0になってほしい入力パターンは接続しないでおけばそれで良いのである。たとえば, (A, B, C) = (0, 0, 0)または(1, 1, 1)のみ1を出力し、それ以外は0を出力するロジックはaとhの出力を同じORゲートに入力させ、それ以外は接続せずにおけばもうほしい回路が完成する。それが以下の図である。

このように、ANDとORの接続を自由に組み替えるだけで簡単に求めているロジックを実装することができる。（もっともこの回路はもっと簡単な回路で表現できるかもしれないが・・・）

あとがき
ANDアレイをいう表題だと一般的すぎて良くないような気もしている。しかしまさにこの記事のような回路のことをANDアレイと呼ぶのかもしれないし、そのへんの言葉の定義の理解がまだ私はあやふやである。

デコーダー、マルチプレクサ

ハードウェア Introduction to Computing Systems
デコーダー

N本の入力ピンがあり、かつ入力のパターンが一つだけ1で残りが0となるようなとき、その入力を2進数の信号に変換する回路をエンコーダー回路とよぶ。入力がN本ならば、N通りの2進数が表現できればいいので出力ピンの本数は\log_{2}{N}＜Mを満たす整数M本のピン数（桁数）があればよい。例えば、N=10本のとき、出力ピン数は\log_{2}{10}＜Mを満たす整数M、\log_{2}{10}=3.321\ldotsであるからM=4本の出力ピンがあれば良い。さらに入力パターンの1となるピンに0~9の数字を対応させると、10進数を2進数に変換できる。一般的に2進数に対応させることを符号化またはエンコードと呼ぶ。エンコードの逆の処理をデコードと呼ぶ。

ここではデコーダー回路を考える。デコーダー回路は2進数を表す入力パターンを、一つが1で残りが0の出力パターンに変換する回路である。入力が2本（2桁の２進数）のとき、真理値表は以下のようになる。

Input A_{1} A_{2} A_{3} A_{4}
00 1 0 0 0
01 0 1 0 0
10 0 0 1 0
11 0 0 0 1

そして回路図は以下のようになる。入力A, BのうちAが２進数1桁目、Bが2進数2桁目となる。これは入力の桁数が3桁, 4桁, ・・・となっても考え方は変わらない。


マルチプレクサ

複数の入力があったとき、それらのうち一つの信号を出力する回路をマルチプレクサと呼ぶ。その回路の一例を下図に示す。これは入力がA, Bの2つの場合で出力がCである。そしてSの信号がどの入力を選択して出力するかに影響する。

S=0のとき、aのANDゲートには1が入力され、bには0が入力される。そうすると、Aの信号はaの出力に反映され、Bは如何なる信号もbから出力されない。そしてaの出力がORゲートを通りCから出力される。これはAの信号が選択されて出力されることを意味する。

S=1のときには、aには0が入力され、bには1が入力される。さっきとは逆にAは如何なる信号もaから出力されず、Bはbの出力に反映される。そしてbの出力はORゲートを通ってCから出力される。つまりBの信号が選択されて出力されている。

ストレージ基礎（Dラッチ）

ハードウェア Introduction to Computing Systems

SRラッチでは1bitのデータを保存できることを見た。利便性を考えると、セットするタイミングとリセットするタイミングをコントロールしたい。つまり、ある特定のタイミングだけ入力を受け取れるようにして、それ以外は入力に影響されないような回路を作りたい。そこで以下の回路を考える。

見てわかる通り、INに入力がない場合はR=1, S=0であるのでQ = 0, \overline{Q} = 1となる。逆にINに入力があるときはR=0, S=1でQ = 1, \overline{Q} = 0となるが、そこからINの入力が0になるとまたQ = 0, \overline{Q} = 1に戻ってしまう。これではラッチの機能を果たせない。しかしIN入力の信号１つだけでラッチの状態をセットしたい。目標はIN入力の信号を通してSRラッチの状態をセットした後に、ラッチの入力を無視する（ラッチの状態を固定できる）ような回路を組むことである。
まず準備として以下の回路を考えてみる。

R, Sの入力は通常のSRラッチと変わらないがR, SはそれぞれENという信号とともにANDゲートの入力になっている。これはENの入力が０のときは如何なるR, Sの入力も無視されることを意味する。ENはEnableの略で、ENが1でないときはこのSRラッチに状態をセットできないということである。これを先程の回路と組み合わせると目的の回路が実装できそうだ。それが以下の回路である。

INにはSRラッチにセットしたい値（1ならセット、0ならリセット）を入力し、ENには1を入力するとSRラッチに状態をセットできる（1bit記憶できる）。その後ENに0を入力するとINに何を入力してもSRラッチの状態は維持される。つまりSRラッチに値を記憶したいときだけENを1にすれば良いということである。このような回路をDラッチと呼ぶ。

ストレージ基礎（SRラッチ）

ハードウェア Introduction to Computing Systems

ORゲートで下記のような回路を組むことを考える。

まず出力Cが0の場合、Bには0が入力されている。B=C=0ならば当然Aも0であり、A=0のままであればCは変化しない。当たり前であるが、状態は変化しない。

この状態から、Aの値を0→1に変化させること考える。ORゲートは入力に一つでも1が入力されると1が出力されるのでCも0→1に変化する。C=1になることによりB=1になるので結果的にA, Bともに1になる。それはCが1であることに矛盾しないので最終的にC=1の状態で安定する。

そこでAを1→0に変化、つまり元の状態に戻してみる。C=B=1の状態であったのでA=０であってもORゲートは1を出力するのでCの値は変化せずC=1のままである。

この後、またAを0→1と変化させてもCの値は変化しない。

つまり、Aの入力を0→1に変化させるとCも0→1に変化するが、その後Aを1→0に戻してもC=1を維持し続ける、ということでこの回路はAの入力の変化の履歴を（一回限りであるが）保存するといえる。別の言い方では、状態が変化し別の状態に変化したとも言える。この場合ならC=0の状態からC=1の状態に変化し、その状態の変化で物事が保存されたと認識することができた（そして元の状態には戻らない）。

上記のような出力が入力の一部に影響を与えることをフィードバックループと呼ぶ。フィードバックを用いると状態の遷移を作り出すことができそうだ。

SRラッチ

そこで以下のような回路を考える。


初期状態

まずa=1, b=0の状態を初期状態とする。そのときB=0であるからa=1であるためには上のNORゲートの動作によりR=0である。またA=1であるが、下のNORゲートの出力0を満たすためにはSは1, 0いずれかである。ここではこの回路になにも入力していない状況を考えるとしてS=0とする。a=1, b=0ならばS=0, R=0であることがわかる。またここからS=1を入力してみても出力(a, b)は(1, 0)から変化しない。ここで出力(a, b)=(1, 0)をSET状態と呼ぶことにする。

RESET

ここで入力(R, S)=(1, 0)を入力してみる。すると上のNORゲートの入力がR=1, B=0になるので出力は0となる。そしてA=0となり下のNORゲートの入力がS=0, A=0となるので出力bが1となる。つまり出力(a, b)が(1, 0)から(0, 1)の状態に遷移する。そしてここから(R, S)=(0, 0)に変化させても、(a, b)=(0, 1)の状態から変化しない。この状態をRESET状態と呼び、このような入力を与えることをRESETするという。

SET

RESET状態に対して(R, S)=(0, 1)を入力してみる。下のNORゲートにはS=1, A=0が入力されているのでb=0に変化する。そして上のNORの入力がB=0, R=0になるのでa=1となり(a, b)=(1, 0)の状態へ遷移し、SET状態になる。このような入力を与えることをSETするという。

SET状態とRESET状態の２つの状態を持ち、(R, S)の入力によって自由に切り替えることができる事がわかる。そして、その状態は入力を与えない限り保持し続ける。このような回路をSRラッチ回路と呼ぶ。この２つの状態をONとOFFに見立てると1桁の2進数を表しているわけなので、SRラッチは1bitの情報を保存することができるといえる。
ラッチとはかんぬきのことで、LOCK状態とUNLOCK状態を持ち、いずれかの状態を保持しつづけるわけで比喩的にラッチという言葉が用いられている。


SRラッチをシンボル化したものが以下の図である。

入力(S, R)の2端子、出力(Q, \overline{Q})の2端子の素子となる。Q, \overline{Q}は前述のa, bに対応する。